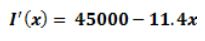Matemáticas Administrativas
UNIDAD 1 Funciones y sus aplicaciones
Bienvenido(a) a la unidad 1, en
ella analizarás el concepto de
función, así como los diferentes
tipos de funciones y las
operaciones que se pueden
realizar con ellas, lo que es
indispensable para comprender
las siguientes unidades temáticas
que abarcan los conceptos de
cálculo diferencial e integral.Sabias que las matemáticas administrativas ofrecen al empresario la posibilidad de responder preguntas tan importantes como:
»¿Cuál sería mi utilidad por la producción de X piezas?
»¿Cuál sería el costo de producir X piezas?
»¿Cuál es el número de piezas que debo producir para no tener pérdidas en mi empresa?
Y aunque la respuesta se puede considerar tan simple como un número, los números sólo se obtienen a través de números.
Introducción
Las matemáticas son una herramienta que permite verificar, mediante modelos gráfico-numéricos, los efectos que pueden generar las variaciones de los elementos o factores que intervienen en los fenómenos y sucesos que se presentan a lo largo de nuestra vida. En esta primera unidad se presenta el concepto de función, así como las diversas formas para su representación.Se analizarán también los tipos de funciones, la graficación y las operaciones que pueden haber entre ellas, con el fin de crear bases sólidas que permitan dar solución práctica a los diversos problemas que se presentan en el área económico-administrativa. Todo esto se podrá realizar a través del análisis de situaciones de optimización, costo total, ingreso, oferta y demanda, y mediante el uso de los diferentes tipos de funciones y modelos gráficos.
Funciones y variables
La relación funcional o función ayuda a describir de manera práctica situaciones que están presentes en la vida real, en las que un valor o cantidad que varía depende de la función o determina el valor de otra, por ejemplo:¿Qué otros ejemplos se te ocurren? Como te darás cuenta, las matemáticas se encuentran en la vida cotidiana y las funciones se usan hasta en la más mínima acción
De ahí se observa que se pueden tener variables o valores que dependen o cambian cuando un valor determinante varía. Otro ejemplo representativo es el puntaje obtenido en un juego de tiro al blanco, en el que hay dibujados en un tablero 5 círculos concéntricos y en cada uno se pueden tener los siguientes valores: 5, 10, 15, 20, 25, iniciando desde el exterior hasta el centro del tablero, como se muestra en la imagen.
Es decir, que la máxima puntuación se obtiene atinándole al círculo que queda en el centro del tablero (25 puntos), y va disminuyendo conforme se aleja hacia la orilla, así se obtienen dos conjuntos, uno correspondiente a los círculos y que se definirá como el conjunto C, y el otro correspondiente a la puntuación y que se llamará P, esto es:
C = {1, 2, 3, 4, 5}
P = {5, 10, 15, 20, 25}
En ambas representaciones se puede comprobar que para cada elemento del conjunto P (puntuación) hay un solo valor o elemento que le corresponde del conjunto C (círculo), es decir, que se cuenta con las siguientes parejas ordenadas:
(1, 5), (2, 10), (3, 15), (4, 20), (5, 25).
Otra forma de representación es mediante un modelo matemático, si consideramos los datos del ejemplo anterior, se observa que si se acierta en el círculo del centro se tendrán 25 puntos y en el círculo más alejado del centro se obtendrán 5 puntos, así se observa que existe una situación de dependencia en la que el puntaje dependerá de a qué círculo del tablero se acierte y cada acierto tiene un valor que resulta de multiplicar el número del circulo al que se acierta por cinco.
Para llevar a cabo esta operación es necesario conocer el número de círculo al que se acierta por lo que se puede decir que el número de círculo es el valor que alimenta al modelo matemático, es decir, que son los valores de entrada y son a los que hay que multiplicar por cinco, para que dé el resultado del puntaje obtenido, lo que dará los valores de salida, si se utilizan además variables que permitan identificar a cada uno de los valores, es decir y para el puntaje y x para los círculos, podremos obtener la siguiente expresión:
y=5x
|
En
donde y corresponde a una variable dependiente y x a una
variable independiente, que conforman lo que se conoce como función.
|
Material de apoyo:http://www.eduteka.org/MI/master/interactivate/index.php
Conceptos relacionados a las funciones variables dependientes e independientes.
Función
|
Variable Dependiente
|
Variable Independiente
|
Es la correspondencia entre dos conjuntos: uno de valores de entrada
y otro de valores de salida, en donde existe una regla de operación que
determina para cada valor de entrada un solo valor de salida.
|
Es aquella cuyo valor, propiedad o característica se trata de cambiar
mediante la manipulación de la variable independiente.
|
Es aquella que es manipulada en un experimento o evento con el objeto
de estudiar como incide sobre la variable dependiente, esto significa que las
variaciones en la variable independiente repercutirán en variaciones en la
variable dependiente.
|
A continuación, se muestran los nombres de las partes de una función; se utiliza la expresión matemática y=5x.
Esta expresión, completa, relaciona una variable independiente con una variable dependiente.
La “y” es la llamada variable dependiente, pues su valor dependerá de los valores que asignemos a la variable “x”. Por ejemplo, si decidimos dar un valor de x=4, la “y” tomará un valor: y=5(4)=20. Para cada valor quedemos a “x”, “y” tomará a su vez un valor. Por lo tanto, la “x” es lo que conocemos como variable independiente, pues el valor que toma no depende de ninguna otra variable y podemos decidirlo. La expresión completa que contiene a ambas variables, es lo que llamaremos función
Tipos de funciones y su aplicación
Como se vio en el tema anterior, la función es la correpsondecia de las variables dependientese independientes, y a partir de las expresiones algebraicas, existen diferentes tipos de funciones, las cuales se verán a continuación.
Función constante: es aquella que tiene la forma :
En donde c es un número real.Ejemplo:
Sea f(x) = 10, debido a la forma de la función, a la variable x se le puede asignar cualquier valor que se desee, sin embargo, el resultado de la función será siempre 10.
Observa la gráfica que se obtiene a partir de la tabla, se presenta una recta paralela al eje de las X (abscisas) y que f(x)=10, corta el eje de las Y (ordenadas) en el punto (0,10)
En este caso, la x toma los siguientes valores: -15, -10, -5, 0, 5, 10, 15.
La variable independiente toma siempre el mismo valor (la función es constante e indica que y=10). Se forman entonces 7 pares ordenados (x,y), que son: (-15, 10), (-10, 10), (-5, 10), (0, 10), (5, 10), (10, 10), (15, 10). Hay que recordar que la variable independiente, x, puede tomar valores no enteros, por lo que existe una infinidad de pares ordenados aunque no se encuentren expresados en la tabla que se presenta. La gráfica es una línea recta horizontal (paralela al eje de las x), que como la función lo indica, pasa por (0, 10). Esta gráfica nos muestra cómo luce una función lineal.
Tipos de funciones y sus gráficas
A continuación se te presentarán los diversos tipos de funciones y sus gráficas:Función lineal
Ejmeplo:
Sea f(x) = 2x + 4, se observa que se trata de una función lineal en donde:
m = 2
b = 4
es decir, que cuando x = 0, f(x) = y = 4.
Observa la siguiente representación gráfica:
Así, se observa que la gráfica es una línea recta creciente, esto se debe a que m > 0, por lo que conforme “x” aumenta, también lo hace ”y”, por lo tanto, se trata de una función creciente.
En este caso, la x toma los siguientes valores: -3, -2, -1, 0, 1, 2, 3. La variable dependiente toma valores que dependen efectivamente de la variable independiente.
Por ejemplo, para x=-3, y = 2(-3)+4 = -6+4 = -2.
Para x=-2, y = 2(-2)+4 = -4+4 = 0.
Para x=-1, y = 2(-1)+4 = -2+4 = 2.
Para x=0, y = 2(0)+4 = 0+4 = 4.
Para x=1, y = 2(1)+4 = 2+4 = 6.
Para x=2, y = 2(2)+4 = 4+4 = 8.
Para x=3, y = 2(3)+4 = 6+4 = 10
Función cuadrática
Una función cuadrática es aquella que tiene la forma:
En donde a,b y c son números reales.
La forma de la gráfica de una función cuadrática es una parábola, en donde el vértice es el punto más bajo si la parábola abre hacia arriba y el vértice es el punto más alto cuando la parábola abre hacia abajo.
Gráficamente la función cuadrática sería como se muestra a continuación:
Observa que la gráfica es una parábola que abre hacia arriba y que su punto mpas bajo se encuntrá en las coordenadas del vértice: (-2,-6).
En este caso, la x toma los siguientes valores: -3, -2, -1, 0, 1, 2, 3. La variable dependiente toma
valores que dependen efectivamente de la variable independiente.
Por ejemplo, para x=-3
Se forman entonces 7 pares ordenados (x, y), que son: (-3, -5), (-2, -6), (-1, -5), (0, -2), (1, 3), (2,
10), (3, 19). Hay que recordar que las variables “x” e “y”, pueden tomar valores no enteros, por lo
que existe una infinidad de pares ordenados aunque no se encuentren expresados en la tabla
que se presenta. La gráfica es una parábola. Esta gráfica nos muestra cómo luce una función
cuadrática.
Función Polinominal
Una función es polinominal si:
El valor de n determina el grado de la función polinomial, que puede ser lineal, cuadrática, cúbica, de cuarto grado, de quinto grado, etc., dependiendo del valor de n, es decir, el valor más alto del exponente de la función es el que determinará de qué grado es la función.
Función racional
Una función racional es el cociente de dos funciones polinomiales y se representa como:

donde q(x) ≠ 0 .
Se presentas un plano cartesiano, y una tabla de datos correspondiente a las variables dependientes e independientes cuando:
En este caso, la x toma los siguientes valores: -3, -2, -1, 0, 1, 2, 3. La variable dependiente toma valores que dependen efectivamente de la variable independiente.
Función exponencial
Una función exponencial es aquella en la que la variable independiente se encuentra como exponente de un número constante.
En este caso, la x toma de los siguientes valores: 2,-1,0,1,2,3. La variable dependiente toma valores que dependen efectivamente de la variable independiente.
Por ejemplo, para x= -2
Se forman entonces 6 pares ordenados (x, y), que son: (-2, 0.25), (-1, 0.5), (0, 1), (1, 2), (2, 4), (3, 8). Hay que recordar que las variables “x” e “y”, pueden tomar valores no enteros, por lo que existe una infinidad de pares ordenados aunque no se encuentren expresados en la tabla que se presenta. Esta gráfica nos muestra cómo luce una función exponencial.
Función logaritmica
Una función logarítmica se define como la inversa de la exponencial y puede ser representada de la siguiente manera:
En este caso, la x forma de los siguientes valores: 0.25,0.5,1,2,4,8. La variable dependiente toma valores que dependen efectivamente de la variable independiente.
Por ejemplo, para x= -2
Se forman entonces 6 pares ordenados (x, y), que son: (-2, 0.25), (-1, 0.5), (0, 1), (1, 2), (2, 4), (3, 8). Hay que recordar que las variables “x” e “y”, pueden tomar valores no enteros, por lo que existe una infinidad de pares ordenados aunque no se encuentren expresados en la tabla que se presenta. Esta gráfica nos muestra cómo luce una función exponencial.
Función logaritmica
Una función logarítmica se define como la inversa de la exponencial y puede ser representada de la siguiente manera:
En este caso, la x forma de los siguientes valores: 0.25,0.5,1,2,4,8. La variable dependiente toma valores que dependen efectivamente de la variable independiente.
Por ejemplo, para x=0.25
Se forman entonces 6 pares ordenados (x, y), que son: (0.25, -2), (0.5, -1), (1, 0), (2,1), (4,2), (8, 3). Hay que recordar que las variables “x” e “y” pueden tomar valores no enteros, por lo que existe una infinidad de pares ordenados aunque no se encuentren expresados en la tabla que se presenta. Esta gráfica nos muestra cómo luce una función logarítmica.
Como puedes ver, cada una de las funciones tiene una representación gráfica que puede mostrar el comportamiento de una actividad o fenómeno en cualquier ámbito de tu vida.
Ingreso, costo, utilidad y punto de equilibrio.
Relacionado con la administración, es importante que conozcas y sepas aplicar las funciones matemáticas, ya que en algún momento de tu vida laboral te encontrarás con ellas.
Ejemplo:
Un punto de equilibrio es usado comúnmente en las empresas u organizaciones para determinar la rentabilidad de vender X producto.
¿quieres saber cómo? Se te invita a estudiar los siguientes conceptos:
Es importante mencionar que la función de ingresos también puede seguir cualquier otro comportamiento algebraico: cuadrático, lineal, exponencial, entre otros.
Ejemplo:
Costo:
La función de costo total se define como:
c(x)= Costo variable por unidad x + Costos Fijos
Ejemplo:
El planteamiento es: Una maquiladora de pantalones de mezclilla ha calculado que sus costos fijos mensuales son de $125,000.00 y que cada pantalón le genera un costo de $35.00.
¿Que hacer? Para determinar el costo total de fabricación en el siguiente mes si se van a elaborar 1500 pantalones de mezclilla.
La solución. Lo primero que se deberá determinar es la función de costo total.
La solución es la siguiente:
C(x)=ax+Cf
Donde: C(x)= función de costo
x = número de artículos o servicios.
En la figura que ilustra la función de costo total e indica que el valor de “a” (el costo de elaboración de un pantalón) es de $35, la variable independiente “x” expresa el número de pantalones y “Cf” representa los costos fijos mensuales con un valor de $125,000.
Sustituyendo en la función de costo total se tiene: C(x)=35x+125000 pesos.
Finalmente, el costo de producción de 1500 pantalones del siguiente mes será de: C(1500)=35(1500)+125000
C(1500)=$177,500 pesos
Otra variante del costo es:
Costo promedio o costo medio: está relacionado con el costo total C(x) de producción o venta de x artículos o servicios y se obtiene al dividir el costo total de entre el número de unidades producidas o servicios ofertados:
Ejemplo:
El planteamiento es: El costo total de producir x libretas escolares por semana sigue el comportamiento de la siguiente función cuadrática:
¿Cuál será el costo promedio de producir 10,000 unidades mensualmente, considere que el mes tiene 4 semanas?
Utilidad
Se obtiene restando los costos de los ingresos:
U(x)= I(x) - C(x)
Ejemplo:
Un fabricante de cremas faciales, mensualmente tiene costos de producción de $15,000.00 y el costo de fabricación por crema es de $4.50. Si cada crema la vende por mayoreo a las tiendas departamentales en $25.00, determine las utilidades que genera en su empresa la venta de cremas faciales si mensualmente vende en exclusiva 2000 cremas a una cadena de SPA.
Solución: si se sabe que las utilidades están representadas por:
U(x) =I(x) - C(x)
Entonces es necesario determinar tanto la función de ingresos como la de costo total, de ahí que en este caso se tienen los siguientes datos:
x = número de cremas
𝐶𝑓= $15,000.00
𝐶𝑣= 4.50x
Cremas vendidas por mes = 2000
p = $25.00
Entonces para los ingresos:
𝐼𝑥=𝑥𝑝
Sustituyendo los datos del problema:
𝑰𝒙=𝟐𝟓𝒙
Y los costos estarán dados por:
𝐶𝑥=𝐶𝑣+𝐶𝑓
Sustituyendo los datos del problema:
𝑪𝒙=𝟒.𝟓𝟎𝒙+𝟏𝟓𝟎𝟎C(x) = 4.5x + 15000
Así sustituyendo en la función de utilidad:
𝑈𝑥=𝐼𝑥−𝐶(𝑥
𝑈𝑥=25𝑥−4.50𝑥+15000
=25𝑥−4.50𝑥−15000
𝑼𝒙=𝟐𝟎.𝟓𝒙−𝟏𝟓𝟎𝟎𝟎𝒑𝒆𝒔𝒐𝒔
Si mensualmente vende 2000 cremas faciales:
𝑈200=20.5(2000 −15000
𝑈200=41000−15000
𝑼𝟐𝟎𝟎=𝟐𝟔𝟎𝟎𝟎𝒑𝒆𝒔𝒐𝒔
Por lo que mensualmente la crema facial genera utilidades de 26,000 pesos.
Punto de equilibrio
Punto de equilibrio: es el punto en que el importe de las ventas de una empresa es igual al de los costos y gastos que dichas ventas originan.
𝑰𝒙=𝑪(𝒙)
Utilidad
Se obtiene restando los costos de los ingresos:
U(x)= I(x) - C(x)
Ejemplo:
Un fabricante de cremas faciales, mensualmente tiene costos de producción de $15,000.00 y el costo de fabricación por crema es de $4.50. Si cada crema la vende por mayoreo a las tiendas departamentales en $25.00, determine las utilidades que genera en su empresa la venta de cremas faciales si mensualmente vende en exclusiva 2000 cremas a una cadena de SPA.
Solución: si se sabe que las utilidades están representadas por:
U(x) =I(x) - C(x)
Entonces es necesario determinar tanto la función de ingresos como la de costo total, de ahí que en este caso se tienen los siguientes datos:
x = número de cremas
𝐶𝑓= $15,000.00
𝐶𝑣= 4.50x
Cremas vendidas por mes = 2000
p = $25.00
Entonces para los ingresos:
𝐼𝑥=𝑥𝑝
Sustituyendo los datos del problema:
𝑰𝒙=𝟐𝟓𝒙
Y los costos estarán dados por:
𝐶𝑥=𝐶𝑣+𝐶𝑓
Sustituyendo los datos del problema:
𝑪𝒙=𝟒.𝟓𝟎𝒙+𝟏𝟓𝟎𝟎C(x) = 4.5x + 15000
Así sustituyendo en la función de utilidad:
𝑈𝑥=𝐼𝑥−𝐶(𝑥
𝑈𝑥=25𝑥−4.50𝑥+15000
=25𝑥−4.50𝑥−15000
𝑼𝒙=𝟐𝟎.𝟓𝒙−𝟏𝟓𝟎𝟎𝟎𝒑𝒆𝒔𝒐𝒔
Si mensualmente vende 2000 cremas faciales:
𝑈200=20.5(2000 −15000
𝑈200=41000−15000
𝑼𝟐𝟎𝟎=𝟐𝟔𝟎𝟎𝟎𝒑𝒆𝒔𝒐𝒔
Por lo que mensualmente la crema facial genera utilidades de 26,000 pesos.
Punto de equilibrio
Punto de equilibrio: es el punto en que el importe de las ventas de una empresa es igual al de los costos y gastos que dichas ventas originan.
𝑰𝒙=𝑪(𝒙)
Consideraciones
|
Si el costo total de producción supera a los ingresos que se obtienen
por las ventas de los objetos producidos o servicios vendidos, la empresa
sufre una perdida.
|
Si los ingresos
superan a los costos, se obtiene una utilidad o ganancia
|
|
Si los ingresos logrados por las ventas
igualan a los costos de producción, se dice que el negocio está en el punto
de equilibrio o de beneficio cero.
|
Gráficamente, el punto de equilibrio es el que está representado por la intersección de las rectas que representan a la función de costos e ingresos.
Si I(x) < C(x), entonces la empresa tiene pérdidas.
Si I(x) = C(x)la empresa no gana ni pierde, está en el punto de equilibrio.
Si I(x) > C(x)la empresa tieneganancias
Cierre de la unidad
En esta unidad analizaste los tipos de funciones y las operaciones que puede haber entre ellas.
El estudio de estas expresiones algebraicas te permitirá dar solución práctica a los diversos problemas que se presentan en el área económico-administrativa, a través del análisis de situaciones de optimización, costo total, ingreso, oferta y demanda, y mediante el uso de los diferentes tipos de funciones y modelos gráficos.
Se ha seleccionadounaseriede recursosenlíneacon el fin de ofrecerteun panorama general de la unidady alternativasencasode quese tedificultela comprensiónde algúnconceptoo proceso.
Si deseas saber más de estos temas se te sugiere revisar las siguientes ligas:
Nota: Para algunas páginas deberás tener instalado el software Java para visualizar la información y realizar actividades.
- Eduteka: http://www.eduteka.org/MI/master/interactivate/index.php
- Universidad Nacional de la Patagonia San Juan Bosco (s.f.). Curso de apoyo en Matemática: http://www.ing.unp.edu.ar/matematica/images/materiales/Modulo_Ingreso.pdf
- Sociedad andaluza de educación matemática THALES. Función cuadrática:http://thales.cica.es/rd/Recursos/rd99/ed99-0416-02/indice.htm
- Descartes. Elementos de una función: http://descartes.cnice.mec.es/materiales_didacticos/Funciones_formas_de_expresar/elementos.htm
- http://es.wikihow.com/calcular-la-utilidad-marginal
- http://dianita-utilidadmarginal.blogspot.mx/2011/10/formula-para-calcular-la-utilidad.html
Bibliografía básica:
- Chiang. (2006). Métodos fundamentales en economía matemática. (4°edición). México: Editorial McGraw-Hill.
- Cissell, R., Cissell, H. y Flaspohler, D. C. (1999). Matemáticas Financieras. (2ª edición). México: Editorial CECSA.
- García, E. (1998). Matemáticas Financieras por medio de Algoritmos, Calculadora Financiera y PC. México: Editorial McGraw-Hill.
- Harshbarger, R. J. y Reynolds, J. J. (2005). Matemáticas Aplicadas a la Administración, Economía y Ciencias Sociales. (7°edición). México: McGraw-Hill.
- Leithold, L. (2006). El cálculo. (7ª edición). Oxford: Editorial Cúspide.
- Motoyuki, A. (2000). Matemáticas Financieras. Córdoba, Argentina: DespeignesEditora.
- Render, B., Stair, R. M. y Hanna, M. E. (2006). Métodos cuantitativos para los negocios.México: Pearson Educación.
- Spiegel, M. R. (1994). Manual de Fórmulas y Tablas Matemáticas. México: McGraw-Hill.
- Thomas. (2006). Cálculo de una variable. Editorial Prentice Hall.
- Toledano y Castillo, M. A. y Himmelstinede Chavarria, L. E. (1984). Matemáticas Financieras. México: Editorial CECSA.
- Vidaurri, H. M. (2001). Matemáticas Financieras. (2ª edición). México: Ediciones Contables, Administrativas y Fiscales -ThomposnLearning
Unidad 2 Límites y Continuidad
Álgebra de límites
Con el álgebra de límites te puedes
aproximar a un valor, ya sea un número
cualquiera o el infinito, de manera exacta.
Así, se puede decir que el límite de una
función describe el comportamiento de una
función f(x) conforme la variable
independiente se aproxima a un valor
constante.
Como pudiste observar, conforme x se acerca a 1 la función es igual a ± 20000, dependiendo de si se va acercando por la derecha o por la izquierda a 1, es decir:
En conclusión se tiene que:
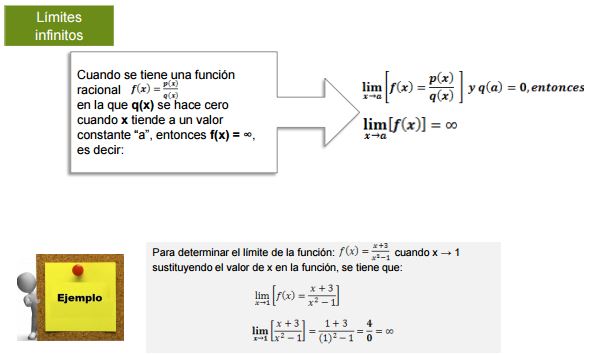
Cuando f(x) se acerca cada vez más a un número Límite (C), conforme x se aproxima a un valor constante “a” por cualquier lado, entonces C será el límite de la función y se escribe:

Conclusión:
El evaluar un límite de una función es tan simple como sustituir el valor hacia el cual tiende x en la función.
El aplicar el álgebra de límites es únicamente aplicar las operaciones de suma, resta, multiplicación, división, raíz n-sima y elevar a una potencia en los resultados obtenidos de las funciones a las que ya se les ha sustituido el valor límite.
Nota: Es importante notar que cuando se divide un número
cualquiera entre ∞ el resultado siempre será cero, ya que el
valor del divisor siempre será mucho más grande que el valor
del número que se quiere dividir.
¿Qué se le podría recomendar al vendedor para que pueda conservar su escala de precios de mayoreo sin que se le presenten problemas económicos con su promoción?
Solución
Se puede observar que la función no está definida en x = 1, esto es porque cuando x toma el valor
de 1, la función tiende al infinito, ya que cualquier número dividido entre cero es igual a infinito.
Como pudiste observar, conforme x se acerca a 1 la función es igual a ± 20000, dependiendo de si se va acercando por la derecha o por la izquierda a 1, es decir:
En conclusión se tiene que:
Cuando f(x) se acerca cada vez más a un número Límite (C), conforme x se aproxima a un valor constante “a” por cualquier lado, entonces C será el límite de la función y se escribe:
Observa la siguiente representación gráfica

En esta última fórmula de igual manera sustituyes el valor de x en la función y posteriormente calculas la raíz n-sima a la que está elevada x.
C o n c l u s i ó n:
El evaluar un límite de una función es tan simple como sustituir el valor hacia el cual tiende x en la función. El aplicar el álgebra de límites es únicamente aplicar las operaciones de suma, resta, multiplicación, división, raíz n-sima y elevar a una potencia en los resultados obtenidos de las funciones a las que ya se les ha sustituido el valor límite.
Existen diferentes límites de una función, a continuación se te muestra el limite de función y su procedimiento.
 El valor de la función puede
crecer o decrecer
indefinidamente, sin embargo,
existen casos en los que la
función adquiere valores reales.
El valor de la función puede
crecer o decrecer
indefinidamente, sin embargo,
existen casos en los que la
función adquiere valores reales.
NOTA:observa que el coeficiente con mayor potencia tendrá como resultado un valor infinito al sustituir el límite en la función.
Ejemplo:
En una fábrica de electrodomésticos se tienen costos fijos de producción de $1’000,000.00 anuales y sus costos específicos son del orden de $430.00 por electrodoméstico. ¿Hasta qué punto puede reducir los costos promedio de producción al aumentar la producción indefinidamente?
Solución:
Se observa que la función de costo tendrá la forma C(x)=430x + 1’000,000, en donde x representa la cantidad de electrodomésticos producidos, de ahí que para determinar el costo promedio de producción se tendrá que dividir la función de costo entre el número de artículos a producir (x):
Ahora bien, con respecto a la derivada del exterior se refiere al exponente fuera del paréntesis que encierra a la función, así, se tomaría como función exterior a:
Y considerando a la función dentro del paréntesis como si fuera una sola variable, así se tiene que la derivada del exterior estaría dad de la siguiente manera:
Finalmente, siguiendo el enunciado que dice que hay que multiplicar la derivada del interior por la derivada del exterior, se tiene que la derivada de:
Y para el caso particular del paquete número 20, se obtiene que:
A continuación se obtiene la función de costo promedio marginal, derivando la función de costo
promedio:
De acuerdo a esto, se tiene que el costo aproximado de producir 1001 de taparroscas será de:
A continuación se muestra gráficamente cómo decrece y crece una función:
Y como f´(1)> 0 entonces la función es creciente en en , para los valores entre
, para los valores entre  , como por ejemplo 1, entonces se tiene que la derivada de la función en ese punto dará:
, como por ejemplo 1, entonces se tiene que la derivada de la función en ese punto dará:
Y como f´(1)>0 entonces la función es creciente en para x=o, se tiene que la derivada de la función en ese punto dará:
para x=o, se tiene que la derivada de la función en ese punto dará:
Y como f´(0) < 0 entonces la función es decreciente en
Es decir, que si se aplica el criterio de la primera derivada para determinar si hay locales extremos locales se tiene:
Criterio de la segunda derivada
Los pasos a seguir para evaluar una función con el criterio de la segunda derivada son:
 es cóncava hacia
arriba o hacia abajo.
es cóncava hacia
arriba o hacia abajo.

Es decir, que si se aplica el criterio de la segunda derivada para determinar la concavidad de la función, se tiene:
Finalmente se puede resumir que para el uso de los criterios de la primera y segunda derivada, es más práctico llenar la siguiente tabla guía:
Dentro de la práctica profesional en las áreas
económico-administrativas, es muy importante la
determinación de maximización de la ganancia o la
utilidad, así como el minimizar los costos de venta y
producción, esto es, en general, optimizar los recursos
de la empresa, es decir, maximizar los beneficios y
minimizar los costos.
Al maximizar el beneficio en cualquier empresa, se puede lograr lo siguiente:
Ahora bien, para determinar el valor máximo en una función se requiere la primera derivada de la función, al igual que se requiere obtener la segunda derivada para determinar el comportamiento de dicha función, esto es, que si se habla de utilidades U(x), ingresos I(x) y costos C(x), entonces se está trabajando con los valores marginales de las funciones, los cuales se muestran representados a continuación.
En esta gráfica observa que:
La utilidad máxima se obtiene cuando bien cuando C´(x)=I´(x) bien cuando I´´(x) < C´´(x)
Se puede observar que los valores marginales de una función son muy útiles, no sólo para conocer los niveles de utilidad, sino para determinar el impacto de las utilidades cuando se presentan variaciones en los insumos.
Y aplicando los criterios de derivada
para obtener los valores máximos,
se comienza por despejar el valor de
x de la ecuación que quedó arriba:
Comprobando que se obtiene un máximo, se calcula la segunda derivada tanto de los ingresos como de los costos:
Es decir, se cumple que:
Si se considera que
, se observa que se verá afectada la variable y, ya que se encuentra en función de los valores que tome x.
Así, cuando la variable x cambia desde un valor inicial , hasta un valor final
, hasta un valor final  , el
cambio se determina calculando la diferencia
, el
cambio se determina calculando la diferencia  , lo que se conoce como cambio o
incremento de una variable y se representa como:
, lo que se conoce como cambio o
incremento de una variable y se representa como:
Y que sirve para determinar los cambios ente una y otra variable y, de manera general, para
determinar los cambios en una función, ya sea de ingreso, costo, demanda o utilidad,
evaluando los valores iniciales y finales en la función correspondiente:
En donde actualmente la demanda de artículos es de 95: 
Es decir, que cuando la empresa tiene una producción de 95 unidades sus gastos son de 30125 pesos. Ahora bien, cuando la producción aumenta a 100 unidades, entonces se tiene que
, por lo que
los gastos finales serán de:
Por lo que:
Así, por la razón de cambio se tiene que:
Con lo que se observa que los gastos de producción por unidad se incrementan en $975.00 pesos por unidad.
Ahora bien, diferenciando implícitamente se tiene:
Aplicando
Se tiene la diferencial de cada parte de la función, así para:
Para:
Para:
Solución
Se puede observar que la función no está definida en x = 1, esto es porque cuando x toma el valor
de 1, la función tiende al infinito, ya que cualquier número dividido entre cero es igual a infinito.
Sin embargo, sí se puede determinar el comportamiento o valores que va tomando la función
cuando x → 1 (x tiende a 1), ya sea con valores más pequeños a uno o bien más grandes a uno: 1 >
x > 1
Como pudiste observar, conforme x se acerca a 1 la función es igual a ± 20000, dependiendo de si se va acercando por la derecha o por la izquierda a 1, es decir:
En conclusión se tiene que:
Cuando f(x) se acerca cada vez más a un número Límite (C), conforme x se aproxima a un valor constante “a” por cualquier lado, entonces C será el límite de la función y se escribe:

Conclusión:
El evaluar un límite de una función es tan simple como sustituir el valor hacia el cual tiende x en la función.
El aplicar el álgebra de límites es únicamente aplicar las operaciones de suma, resta, multiplicación, división, raíz n-sima y elevar a una potencia en los resultados obtenidos de las funciones a las que ya se les ha sustituido el valor límite.
Límite de una función y sus propiedades
Existen diferentes límites de una función, a continuación se te muestra el límite de función y su procedimiento.
A continuación verás ejemplos para el cálculo de límite de una función cuando la variable independiente tiende al
infinito.
NOTA: observa que el coeficiente con mayor potencia tendrá como resultado un valor infinito, al sustituir el límite en la función.
Ejemplo:
En una fábrica de electrodomésticos se tienen costos fijos de producción de $1´000,000.00 anuales y sus costos específicos son del orden de $430.00 por electrodoméstico. ¿Hasta que punto puede reducir los costos promedios de producción al aumentar la producción indefinidamente?
Solución: Se observa que la función de costo tendrá la forma C(x)=430x + 1´000,000.00, en donde x representa la cantidad de electrodomésticos producidos, de ahí que para determinar el costo promedio de producción se tendrá que dividir la función de costo entre el número de artículos a producir (x):
Funciones continuas y discontinuas
Las funciones Continuas son aquellas cuyas gráficas se pueden
dibujar en un solo trazo,
es decir, si no presentan
cortes o puntos de
discontinuidad.
Las funciones Discontinuas Es discontinua si hay
puntos en los cuales
existe una pequeña
variación de la variable
independiente, lo que
genera un salto en los
valores de la variable
dependiente.
Conceptos relacionados a la continuidad y a la discontinuidad en una funcipon.
Según se pudo observar, al realizar el cálculo de límites de una función, no siempre el límite coincide con el valor de
la función en el punto hacia el cual se aproxima la variable independiente, esto es fácil de detectar al graficar la
función en los valores cercanos al límite, ya que la gráfica de la función se puede cortar o tener una interrupción en
algún punto cercano al límite.
Por ejemplo, se tiene la siguiente función:
en la que se dice que x → 1, y que
al graficar las coordenadas que van
acercándose al límite se tiene la
siguiente gráfica
En donde se observa que hay un
punto exactamente cuando x = 1
en el que la gráfica de la línea ya
no continúa con el resto de los
valores, es decir, que hay una
ruptura en la gráfica.
De ahí que se puede definir que una función es continua cuando no se presenta un corte en la línea que
representa su gráfica, mientras que en una función discontinua se presentan cortes en la línea que
representa la gráfica de la función.
Así se tienen tres condiciones que permiten descubrir si una función es continua o discontinua:
- Una función será continua si f(x) está definida en x = a, es decir, que sus valores son reales.
- Una función será continua si el Límite de la función f(x) cuando x → a existe.
- Una función será continua si:
Por lo que si una de las condiciones anteriores no se cumple, la función será discontinua.
Operaciones con funciones continuas
Si las funciones f(x) y g(x) son continuas en un punto a, entonces las funciones podrán sumarse,
multiplicarse o dividirse (para g(x) ≠ 0 en el caso de división).
Toda función polinomial es continua.
Ejemplo:
Oferta y demanda. Un vendedor de aceites orgánicos en frascos de 250 ml vende
aceite de uva a $90.00 cada frasco, pero si le compran más de 10 frascos el precio por
frasco es de $85.00.¿Qué se le podría recomendar al vendedor para que pueda conservar su escala de precios de mayoreo sin que se le presenten problemas económicos con su promoción?
Con lo que se observa que el precio de 10 frascos es
de $900.00 y de 11 frascos es de $935.00, por lo que
para evitar contradicciones, el precio de 11 frascos
debe ser superior al de 10; si se dice que p es el precio
de cada frasco de aceite cuando se compran más de
10 frascos, se debe cumplir que 11p > 900, es decir, p
> 900/11 = $81.81, por lo tanto, el vendedor debe
asignar un precio superior a $81.81 para cada frasco
cuando le compren más de 10 frascos de aceite de
uva.
UNIDAD 2 Límites y continuidad
Álgebra de límites
Con el álgebra de límites te puedes
aproximar a un valor, ya sea un número
cualquiera o el infinito, de manera exacta.
Así, se puede decir que el límite de una
función describe el comportamiento de una
función f(x) conforme la variable
independiente se aproxima a un valor
constante
Como pudiste observar, conforme x se acerca a 1 la función es igual a ± 20000, dependiendo de si se va acercando por la derecha o por la izquierda a 1, es decir:
En conclusión se tiene que:
Cuando f(x) se acerca cada vez más a un número Límite (C), conforme x se aproxima a un valor constante “a” por cualquier lado, entonces C será el límite de la función y se escribe:
Observa la siguiente representación gráfica
Operación para determinar los límites de una función:
Solución: Desarrollo
En la presente fórmula de álgebra de límites se
puede observar que para evaluar el límite de
una función sea f(x), g(x) o cualquiera, se tiene
que sustituir en dicha función el valor del
número hacia el cual tiende x y el resultado
será siempre un número constante.

En esta segunda fórmula se observa que para
sumar o restar dos funciones evaluadas en
el valor hacia el cual tiende x, se puede
obtener de manera independiente el resultado
de cada función al sustituir el valor de x en
cada una y finalmente sumar o restar ambos
resultados según sea el caso.
En el siguiente caso se tiene que para
multiplicar dos funciones evaluadas en el
valor hacia el cual tiende x se puede obtener
de manera independiente el resultado de
cada función al sustituir el valor de x en cada
una y finalmente multiplicar ambos
resultados.
En la siguiente fórmula se tiene que para dividir dos
funciones evaluadas en el valor hacia el cual tiende
x, se puede obtener de manera independiente el
resultado de cada función al sustituir el valor de x en
cada una y finalmente dividir ambos resultados.
En esta fórmula el valor hacia el cual tiende x se
sustituye en la función y posteriormente se evaluará
la potencia a la que está elevada la función.En esta última fórmula de igual manera sustituyes el valor de x en la función y posteriormente calculas la raíz n-sima a la que está elevada x.
C o n c l u s i ó n:
El evaluar un límite de una función es tan simple como sustituir el valor hacia el cual tiende x en la función. El aplicar el álgebra de límites es únicamente aplicar las operaciones de suma, resta, multiplicación, división, raíz n-sima y elevar a una potencia en los resultados obtenidos de las funciones a las que ya se les ha sustituido el valor límite.
Existen diferentes límites de una función, a continuación se te muestra el limite de función y su procedimiento.
 El valor de la función puede
crecer o decrecer
indefinidamente, sin embargo,
existen casos en los que la
función adquiere valores reales.
El valor de la función puede
crecer o decrecer
indefinidamente, sin embargo,
existen casos en los que la
función adquiere valores reales.NOTA:observa que el coeficiente con mayor potencia tendrá como resultado un valor infinito al sustituir el límite en la función.
En una fábrica de electrodomésticos se tienen costos fijos de producción de $1’000,000.00 anuales y sus costos específicos son del orden de $430.00 por electrodoméstico. ¿Hasta qué punto puede reducir los costos promedio de producción al aumentar la producción indefinidamente?
Solución:
Se observa que la función de costo tendrá la forma C(x)=430x + 1’000,000, en donde x representa la cantidad de electrodomésticos producidos, de ahí que para determinar el costo promedio de producción se tendrá que dividir la función de costo entre el número de artículos a producir (x):
Y si lo que se desea conocer es el costo
promedio de producción cuando el nivel
de producción se eleve indefinidamente
se tiene que:
Por lo tanto, el costo
promedio de producción
será de $430.00 cuando el
nivel de fabricación de
productos
electrodomésticos crezca
indefinidamente.
Nota:
Es importante notar que cuando se divide un número
cualquiera entre ∞ el resultado siempre será cero, ya que el
valor del divisor siempre será mucho más grande que el valor
del número que se quiere dividir.
Ejemplo:
El nivel de satisfacción (%) de clientes en un
autoservicio de acuerdo al número de artículos
comprados fue medido a través de la siguiente función:
En donde x representa el número de artículos comprados.
¿Cuál será el nivel de satisfacción del cliente (%) conforme aumentan las compras del cliente?
Solución: Si se considera que el cliente
comprará un número infinito de artículos se
puede observar cuál será el comportamiento
del nivel de satisfacción del cliente en el punto
más alto de sus compras:
Con el fin de eliminar la indeterminación, en el caso de una función racional es conveniente dividir cada
uno de los factores de la función entre la variable independiente con la potencia más alta, así se tiene
que, para este caso en particular.
Por lo que el nivel de satisfacción del cliente será del 83.33% y nunca podrá ser mayor a éste.
Según se pudo observar, al realizar el cálculo de límites de una función, no siempre el límite coincide con el valor de
la función en el punto hacia el cual se aproxima la variable independiente, esto es fácil de detectar al graficar la
función en los valores cercanos al límite, ya que la gráfica de la función se puede cortar o tener una interrupción en
algún punto cercano al límite.
Por ejemplo, se tiene la siguiente
función:
en la que se dice que x → 1, y que
al graficar las coordenadas que van
acercándose al límite se tiene la
siguiente gráfica:
En donde se observa que hay un
punto exactamente cuando x = 1
en el que la gráfica de la línea ya
no continúa con el resto de los
valores, es decir, que hay una
ruptura en la gráfica.
De ahí que se puede definir que una función es continua cuando no se presenta un corte en la línea que
representa su gráfica, mientras que en una función discontinua se presentan cortes en la línea que
representa la gráfica de la función.
Así se tienen tres condiciones que permiten descubrir si una función es continua o discontinua:
Una función será continua si f(x) está definida en x = a, es decir, que sus valores son reales.
Una función será continua si el Límite de la función f(x) cuando x → a existe.
Una función será continua si:
Por lo que si una de las condiciones anteriores no se cumple, la función será discontinua.
Operaciones con funciones continuas
Si las funciones f(x) y g(x) son continuas en un punto a, entonces las funciones podrán sumarse,
multiplicarse o dividirse (para g(x) ≠ 0 en el caso de división).
Toda función polinomial es continua.
Ejemplo:
Oferta y demanda. Un vendedor de aceites orgánicos en frascos de 250 ml vende
aceite de uva a $90.00 cada frasco, pero si le compran más de 10 frascos el precio por
frasco es de $85.00.
¿Qué se le podría recomendar al vendedor para que pueda conservar su escala de
precios de mayoreo sin que se le presenten problemas económicos con su
promoción?
Solución: Si se define como p(x)
a la función de precio de x
frascos de aceite de uva, se
tiene la siguiente función:
El modelo gráfico que representa a esta función de oferta vs demanda es:
Con lo que se observa que el precio de 10 frascos es
de $900.00 y de 11 frascos es de $935.00, por lo que
para evitar contradicciones, el precio de 11 frascos
debe ser superior al de 10; si se dice que p es el precio
de cada frasco de aceite cuando se compran más de
10 frascos, se debe cumplir que 11p > 900, es decir, p
> 900/11 = $81.81, por lo tanto, el vendedor debe
asignar un precio superior a $81.81 para cada frasco
cuando le compren más de 10 frascos de aceite de
uva.
Cierre de unidad
En esta unidad estudiaste el concepto de límite y cómo es que describe,
de forma precisa, el comportamiento de una función cuando los valores
de la variable independiente están muy próximos a un valor constante,
además de su utilidad en los procesos económico-administrativos, tales
como rendimiento y producción máxima.
También pudiste observar cuando una función es continua, su aplicación
en procesos productivos y su impacto en los costos de producción.
La solución de problemas de límites y continuidad de una función te
permitirán determinar su impacto en los procesos económicoadministrativos,
como pudiste observar en los ejemplos que se te
proporcionaron.
UNIDAD 3 Cálculo Diferencial y sus aplicaciones.
La derivada
El modelado de los procesos económico-administrativos está
asociado a la identificación del valor que optimiza a una
función, esto es, que si se trata de un problema de costos se
requiere conocer el costo mínimo y el valor para el que se
produce, así como para ingresos y utilidades es de interés
saber cómo se alcanzan los valores máximos que se pueden
tener a partir de una producción o venta, ya sea de un producto
o servicio
Así es como se ve la importancia de la derivada dentro de los
problemas de optimización y sus aplicaciones en las
situaciones de oferta, demanda, elasticidad y productividad.
La derivada
Es la representación del cambio infinitesimal de na función a medida que va cambiando el valor de la variable independiente, así la derivada de una función f(x) se representa como f’(x), que se lee: f prima y se define para
cualquier función f(x) de la siguiente manera:
En donde:
- Δx y Δy: incrementos de las variables x, y, respectivamente.
representa a la razón o tasa promedio de cambio de y con respecto a x en el intervalo (x1 , x2), esto es que tanto varia el valor de y por cada unidad de cambio x.
se interpreta como la razón o tasa instanténea de cambio de y con respecto a x, en el punto a x1.
De manera práctia la notación para la derivada es:
Reglas y fórmulas de derivación:
Al igual que con los límites existen fórmulas y reglas que permiten calcular las derivadas de funciones algebraicas, para lo cual se presenta a continuación un formulario en el que se deberá tomar en cuenta que:
- u,v,w: son funciones cuya variables independiente es x.
- a,b,c,n: son números constantes
- e: 2.71828...
- Ln u: es el logaritmo natural de u, en donde u > 0.
Reglas y fórmulas de derivación:
Ejemplo de las derivadas:
A continuación se resuelven las derivadas de algunas funciones utilizando las fórmulas y reglas de derivación:
Regla de cadena:
Es aplicada cuando se tiene una función dentro de una función elevada a una potencia, sea la siguiente función:
Sin embargo, una manera más fácil de interpretarla es mediante el siguiente
enunciado:
Calcular la derivada de la función en el interior del paréntesis y multiplicarla
por la derivada del exterior.
Es decir, si se toma en cuenta la función mostrada en el ejemplo, se tiene que:
Y considerando a la función dentro del paréntesis como si fuera una sola variable, así se tiene que la derivada del exterior estaría dad de la siguiente manera:
Finalmente, siguiendo el enunciado que dice que hay que multiplicar la derivada del interior por la derivada del exterior, se tiene que la derivada de:
Como se vio anteriormente, la razón o tasa promedio de cambio se define como:
Ejemplo: Considerando que la oferta a “O” de un determinado artículo
en función del precio “p” sigue la siguiente función:
Determine ¿cuál será la razón promedio de cambio en la oferta cuando el precio varía de p=10 a p=11?
Solución: De acuerdo
a la definición de razón
o tasa promedio de
cambio, se tiene que:
Asimismo, la razón o tasa
instantánea de cambio se
define como:
Ejemplo:
Tomando en cuenta los datos del problema anterior, determine ¿cuál será la razón de cambio en la oferta con respecto al precio de venta, cuando p=0 (cambio instantáneo)?
Solución:De acuerdo con la definición de razón o tasa cambio instantánea, se tiene que calcular la derivada de la función de oferta:
Por lo que cuando el precio de venta es: p= 10, la razón de cambio instantáneo será:
0´(10) = 14 (10) = 140
Es decir que, cuando el precio es de 10, la ofera cambia en 140 unidades cuando el precio cambia una unidad.
Hasta ahora se ha calculado la primera derivada de una función, sin embargo, también es posible,
siempre que no se llegue a un valor de cero, obtener la segunda, tercera, cuarta, quinta,… y n-sima
derivada de una función.
Ingreso marginal:
Describe cómo se ven afectados los ingresos por
cada unidad nueva que se produce y se vende, y se
determina como la derivada de la función de
ingresos, lo que representa una aproximación del
ingreso real cuando se vende una unidad más de
cierto producto o servicio.
Así, considerando que representa a los ingresos obtenidos al vender x número de artículos, el
ingreso marginal muestra cuál será el ingreso que se obtiene al vender el artículo x + 1, esto es:
I(x+1)- I(x)
Es decir, los ingresos de venta de x número de artículos incrementada en 1, menos los ingresos de
la venta de x artículos.
Finalmente, cómo se considera el incremento de unidades de artículos, esto es: x= 1 lo que
implica una razón de cambio de los ingresos cuando aumenta la producción en una unidad; es
decir:
Ejemplo:
Una compañía turística tiene un ingreso mensual en la venta de sus paquetes regionales representado por la siguiente función:
Hasta el día de hoy, la compañía ofrece 20 paquetes vacacionales, sin embargo, planea aumentar a 21 el número de paquetes que ofrece. ¿Cuál será el ingreso que generará la implementación y venta del paquete vacacional número 21?
Este valor sería una aproximación al ingreso que generaría por incorporar en sus paquetes regionales el paquete 21.
Sin embargo, si se desea conocer cuál sería el ingreso exacto al incorporar y vender el paquete 21, se tiene que:
Ya que dentro de esta operación ya esta incorporando el paquete 21, en (x+1), entonces se sustituye x por 20 en al expresión encontrada:
Que representaría el ingreso exacto al incorporar y vender el paquete 21 en la lista de
paquetes turísticos regionales en la compañía turística.
Costo marginal:
Es la derivada de la función de costo: el calor que se o obtiene es una
aproximación al costo
verdadero cuando se
produce o genera una
unidad más de cierto
producto o servicio.
Así, si se requiere saber el costo
que implica el producir x
unidades de un artículo más una
unidad, es recomendable recurrir
a la derivada del costo y de
manera similar al ingreso
marginal se tiene que para los
costos marginales se cumple:
Determina cómo será el costo de producir 200 tarjetas con respecto a la producción de una tarjeta más
De acuerdo a esto, se tiene que el costo aproximado de producir 201 tarjetas de felicitación será de:
Ahora bien, ya que se requiere conocer cómo es el costo aproximado con respecto al real,
se tiene que:
Sustituyendo ahora el valor de x= 200, para así obtener el costo de producción de 201 tarjetas de felicitación
Con lo que se observa que la diferencia entre el costo exacto y el costo marginal es mínima: 0.8005 pesos, así se puede concluir que con el costo marginal también se obtienen resultados confiables al igual que con la fórmula de ingreso marginal.
Costo promedio o medio marginal
Es la derivada de la función de costo promedio: el valor que se obtiene es una medida de la razón de cambio de la función de costo promedio en función del número de unidades o servicios producidos/vendidos.
Ejemplo: El costo total de producción mensual de x número de taparroscas para envases de agua embotellada está dado por:
Determine cómo será el costo de producir la unidad 1001 de taparroscas si actualmente se produce 1000 tapas por mes
Solución: Primero se determinará la función de costo promedio:
De acuerdo a esto, se tiene que el costo aproximado de producir 1001 de taparroscas será de:
Utilidad marginal:
Es la derivada de la función de utilidad: U´(x) y es una aproximación a la
utilidad obtenida de la producción y venta de una unidad más de cierto
producto o servicio.
Así, si se requiere saber cuáles son las utilidades que generará el producir
x unidades de un artículo más una unidad, es recomendable recurrir a la
derivada de las utilidades, con lo que se demuestra que:
Ejemplo:
En una fábrica se determinó que cuando se producen x número de artículos, se tenía que:
Y cada artículo vendido generaba ingresos de $10.00 pesos.
Determine las utilidades que se generarán si se producen y venden 100 unidades.
Solución. Primero se determinará la función de utilidad, si se sabe que:
En donde para este caso:
Se tiene que:
Por lo que la utilidad marginal será:
De acuerdo a esto, se tiene que las utilidades generadas aproximadamente al producir 100 artículos serán de:
Lo que significa que se tienen -63.34 miles de pesos de pérdidas en este proceso
Utilidad marginal:
La elasticidad de la demanda, η, es una aproximación del cambio porcentual de la demanda y es originado por un incremento del 1% en el precio y está representada por la siguiente fórmula:
Y se interpreta de la siguiente manera:
Ejemplo:
Si la demanda y el precio de ciertos envases de plástico están representados por:
q= 930 - 5p
Para 0 ≤ p ≤, determine el punto de elasticidad de la demanda en
que es elástica la demanda, en función de los precios de los envases
de plástico.
Solución: Se sabe que:
En donde para este caso en particular
Así, la elasticidad de la demanda será:
Ahora bien, la demanda de los envases será elástica si:
Por lo que la demanda será elástica cuando el precio sea superior a 93.
Cálculo de máximos y mínimos:
Generalmente en nuestra vida estamos buscando formas para
resolver problemas. Las matemáticas y en particular el cálculo
diferencial nos ayudan a encontrar las respuestas que estamos
buscando.
Entre los valores que puede tener una función (y) puede haber
uno que sea el más grande y otro que pueda ser más pequeño.
A esto valores se le pueden llamar punto máximo y punto
mínimo.
Funciones crecientes y decrecientes
Una función es creciente en el intervalo I, si para dos
números x1, x2 cualesquiera en I, tales que x1 < x2, se
tiene que:
Una funciónA continuación se muestra gráficamente cómo decrece y crece una función:
Criterio de la primera y segunda derivada:
Los criterios de la primera y segunda derivada ayudan a determinar el comportamiento de una función mediante un cálculo exacto y analítico.
Criterio de la primera derivada
Los pasos a seguir para evaluar una función con el criterio de la primera derivada son:
- Obtener la derivada de la función.
- Determinar los valores críticos, esto es, los valores de x en la derivada de la función cuando:
- Se marcan los valores críticos en la recta numérica y se escoge un valor cualquiera entre cada intervalo y se sustituye el valor seleccionado en la derivada, con lo que se determinará el signo de la derivada en esos puntos. Esto se realiza en los intervalos antes y después del valor crítico.
- De acuerdo a los signos obtenidos al evaluar la derivada en cada intervalo, se aplica el siguiente criterio:
- Si los signos son (+)(-), se tiene un máximo local.
- Si los signos son (-)(-), se tiene un mínimo local.
- Si los signos son (+)(+) o (-)(-), no hay extremo local.
Ejemplo:
Considerando el criterio de la primera derivada, determine los intervalos en donde la función:
es creciente o decreciente.
Solución: Aplicando el criterio de la primera derivad se tiene lo siguiente:
Calculando la primera derivada de la función:
Que son las raíces o valores de x, con lo que se puede observar que los intervalos establecidos
para x en la derivada serán (valores críticos en la recta numérica):
Ahora bien, evaluando la derivada de la función en los intervalos establecidos, esto es:
para los valores entre como por ejemplo 1, entonces se tiene que la derivada de la función
en ese punto dará:
como por ejemplo 1, entonces se tiene que la derivada de la función
en ese punto dará:
 como por ejemplo 1, entonces se tiene que la derivada de la función
en ese punto dará:
como por ejemplo 1, entonces se tiene que la derivada de la función
en ese punto dará:
Y como f´(1)> 0 entonces la función es creciente en en
 , para los valores entre
, para los valores entre  , como por ejemplo 1, entonces se tiene que la derivada de la función en ese punto dará:
, como por ejemplo 1, entonces se tiene que la derivada de la función en ese punto dará:Y como f´(1)>0 entonces la función es creciente en
 para x=o, se tiene que la derivada de la función en ese punto dará:
para x=o, se tiene que la derivada de la función en ese punto dará:Y como f´(0) < 0 entonces la función es decreciente en

Es decir, que si se aplica el criterio de la primera derivada para determinar si hay locales extremos locales se tiene:
Criterio de la segunda derivada
- Obtener la segunda derivada de la función
- Determinar los puntos de inflexión, esto es, los valores de x en la segunda derivada de la función cuando
es cóncava hacia arriba o hacia abajo.
- Se marcan los puntos de inflexión en la recta numérica y se escoge un valor cualquiera entre cada intervalo y se sustituye el valor seleccionado en la segunda derivada, con lo que se determinará el signo de la segunda derivada en esos puntos. Esto se realiza en los intervalos antes y después de los puntos de inflexión.
- De acuerdo a los signos obtenidos al evaluar la derivada en cada intervalo, se aplica el siguiente criterio:
- Si f´´(x) > 0, entonces la función es cóncava hacia arriba en ese intervalo.
- Si f´´(x) < 0, entonces la función es cóncava hacia abajo en ese intervalo.
 es cóncava hacia
arriba o hacia abajo.
es cóncava hacia
arriba o hacia abajo.
Solución: Aplicando el criterio de la segunda derivada, se tiene lo siguiente:
Calculado hasta la segunda derivada de la función:
Igualando a cero la segunda derivada de la función:
Que son las raíces o valores de x, con lo que se puede observar que los intervalos establecidos
para x en la derivada serán (puntos de inflexión en la recta numérica):
Ahora bien, evaluando la derivada de la función en los intervalos establecidos, esto es:
para los valores entre  como por ejemplo 5, entonces se tiene que la segunda derivada de
la función en ese punto dará:
como por ejemplo 5, entonces se tiene que la segunda derivada de
la función en ese punto dará:
 como por ejemplo 5, entonces se tiene que la segunda derivada de
la función en ese punto dará:
como por ejemplo 5, entonces se tiene que la segunda derivada de
la función en ese punto dará:
Y como f´´(5) > 0 entonces la función es cóncava hacia arriba en  para los valores entre -2,
para los valores entre -2, como por ejemplo -5, entonces se tiene que la derivada de la función en ese punto dará:
como por ejemplo -5, entonces se tiene que la derivada de la función en ese punto dará:
Y como f´(-5)>0 entonces la función es cóncava hacia abajo en  para los valores entre -2,
para los valores entre -2, como por ejemplo -5, entonces se tiene que la derivada de la función en ese punto dará:
como por ejemplo -5, entonces se tiene que la derivada de la función en ese punto dará:
Es decir, que si se aplica el criterio de la segunda derivada para determinar la concavidad de la función, se tiene:
Finalmente se puede resumir que para el uso de los criterios de la primera y segunda derivada, es más práctico llenar la siguiente tabla guía:
Al maximizar el beneficio en cualquier empresa, se puede lograr lo siguiente:
Ahora bien, para determinar el valor máximo en una función se requiere la primera derivada de la función, al igual que se requiere obtener la segunda derivada para determinar el comportamiento de dicha función, esto es, que si se habla de utilidades U(x), ingresos I(x) y costos C(x), entonces se está trabajando con los valores marginales de las funciones, los cuales se muestran representados a continuación.
En esta gráfica observa que:
La utilidad máxima se obtiene cuando bien cuando C´(x)=I´(x) bien cuando I´´(x) < C´´(x)
Se puede observar que los valores marginales de una función son muy útiles, no sólo para conocer los niveles de utilidad, sino para determinar el impacto de las utilidades cuando se presentan variaciones en los insumos.
Ejemplo:
Una empresa en servicio de telefonía pretende incrementar sus
ventas promocionando sus servicios por televisión, para lo cual
realizó varios estudios para determinar los costos que dicha
publicidad le generará y obtuvieron las siguientes funciones de costo
por publicidad y de demanda de servicios de telefonía:
En donde:
C(x) = costos por servicio de telefonía en función de los costos de publicidad.
p(x) = precio por servicio de telefonía que se presta.
x = número de servicios de telefonía.
Determine la cantidad de servicio que se requiere vender para maximizar la ganancia.
Solución: Considerando la función de demanda, se puede obtener la función de ingresos de la
empresa, recordando que:
Por lo que para este caso en particular los ingresos serán:
Ahora bien, para obtener la máxima ganancia, se requiere de los valores marginales tanto de
los ingresos como de los costos, así para el ingreso marginal se tiene:
Y para el costo marginal:
Y ya que para maximizar la ganancia se requiere que el ingreso marginal sea igual al costo
marginal:Comprobando que se obtiene un máximo, se calcula la segunda derivada tanto de los ingresos como de los costos:
I´´(x) < C´´(x)
Por lo que se obtiene efectivamente la máxima
utilidad.
Por lo tanto, cuando la compañía de servicio
en telefonía da 37,500 servicios, la utilidad
será maximizada.
La diferencial
Es una ecuación en la que intervienen derivadas de una o más funciones. Al trabajar con diferenciales, se compara entre los distintos valores que toman las variables dependiente e independientemente, para así observar y medir los cambios que se originen.
Incremento de una función
, se observa que se verá afectada la variable y, ya que se encuentra en función de los valores que tome x.
Así, cuando la variable x cambia desde un valor inicial
 , hasta un valor final
, hasta un valor final  , el
cambio se determina calculando la diferencia
, el
cambio se determina calculando la diferencia  , lo que se conoce como cambio o
incremento de una variable y se representa como:
, lo que se conoce como cambio o
incremento de una variable y se representa como:
Ejemplo:
Una empresa desea determinar en cuánto deberá incrementar su
nivel de gastos si aumenta la producción debido al aumento en la
demanda de sus artículos, para lo que obtiene la siguiente función:

- Determine en cuánto se incrementarán los gastos si la producción aumenta a 100 unidades.
- Determine la razón de cambio que se dará en los gastos al incrementarse la producción en una unidad.
Es decir, que cuando la empresa tiene una producción de 95 unidades sus gastos son de 30125 pesos. Ahora bien, cuando la producción aumenta a 100 unidades, entonces se tiene que

Esto es, que aumentan en $4 875.00 pesos.
Para determinar la razón de cambio se tomarán en cuenta los datos anteriores, de lo que se observa
que:
Por lo que:
Así, por la razón de cambio se tiene que:
Con lo que se observa que los gastos de producción por unidad se incrementan en $975.00 pesos por unidad.
Diferencial Implícita
La diferencial implícita es un proceso mediante el cual puede obtenerse la diferencial dy cuando se tiene una ecuación y no una función, pudiendo existir más de un elemento de la variable y.
Diferencial Logarítmica
Tomando en cuenta las leyes logarítmicas:
Aplicando las leyes de logaritmos a las funciones es posible aplicar la diferencial logarítmica:
Así, para obtener la diferencial logarítmica dy de una
función es necesario aplicar las leyes de los logaritmos
a la función dada.
Ejemplo:
Empleando la diferencial logarítmica determine a partir de la siguiente función:
Solución:
Aplicando a la función leyes de logaritmos, se tiene:
Aplicando
Se tiene la diferencial de cada parte de la función, así para:
Para:
Para:
Y finalmente para:
Elasticidad
La elasticidad es indicador
de la magnitud que cambiará
la variable dependiente si la
variable independiente se
modifica en una unidad y se
representa como:
Una manera de determinarla es a través de
la diferencial con logaritmos y así obtener:
Ejemplo:
Determine la elasticidad de la demanda si:
Cierre de Unidad
En esta unidad estudiaste el concepto de
la derivada, las fórmulas y los métodos de
derivación, así como el concepto de la
diferencial, el cual te permitirá tener los
conocimientos necesarios para
comprender el análisis marginal y sus
implicaciones en los procesos económicos
y administrativos de una empresa.
Biografía complementaria:
- Cissell, R., Cissell, H. y Flaspohler, D. (1999). Matemáticas Financieras. (2ª edición). México: Editorial CECSA.
- García, E. (1998). Matemáticas Financieras por medio de Algoritmos, Calculadora Financiera y PC. México: Editorial McGraw-Hill.
- Hernández, A. (1998). Matemáticas Financieras Teoría y Práctica. (4ª edición). México: Ediciones Contables, Administrativas y Fiscales.
- Motoyuki, A. (2000). Matemáticas Financieras. Córdoba, Argentina: Despeignes Editora.
- Spiegel, M. R. (1994). Manual de Fórmulas y Tablas Matemáticas. Traducción de la 1° edición. México: McGraw-Hill..
- Toledano y Castillo, M. A. y Himmelstine de Chavarria, L. E. (1984). Matemáticas Financieras. México: Editorial CECSA.
- Vidaurri, H. M. (2001). Matemáticas Financieras. (2ª edición). México: Ediciones Contables, Administrativas y Fiscales - Thomposn Learning.